The MESYS Rolling Bearing Calculation provides tangential stiffness matrices and compliance matrices for rolling bearings. An example of a tangential stiffness matrix for a 6204-C3 deep groove ball bearing with a radial load of 2 kN is shown here:
| ux [µm] | uy [µm] | uz [µm] | ry [mrad] | rz [mrad] | |
| Fx [N] | 6,870908 | 0 | 0 | 0 | -97,8685 |
| Fy [N] | 0 | 124,8287 | 0 | 0 | 0 |
| Fz [N] | 0 | 0 | 54,25732 | 0 | 0 |
| My [Nm] | 0 | 0 | 0 | 0,466423 | 0 |
| Mz [Nm] | -0,09968 | 0 | 0 | 0 | 1,461134 |
The tangential stiffness indicates the amount by which the load changes when the relative displacement is varied from the operating point. With an axial displacement of 1 µm, the axial force increases by 6.9 N and the tilting moment around the z-axis decreases by 0.1 Nm. As the bearing is subjected to a purely radial load here, there is no coupling of the radial and axial components. This is different for radial and axial loads.
The following diagrams show the radial force and the second main diagonal element of the tangential stiffness matrix over the radial displacement of a 6204-C3 for two different axial displacements.
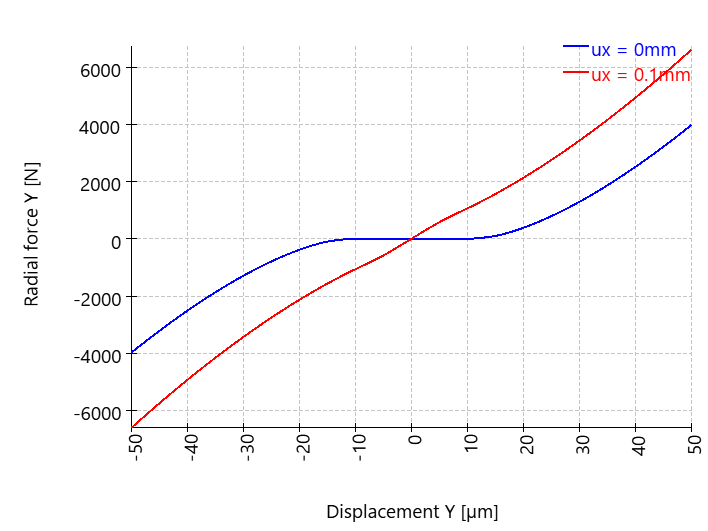
Radial force over radial displacement for two axial displacements
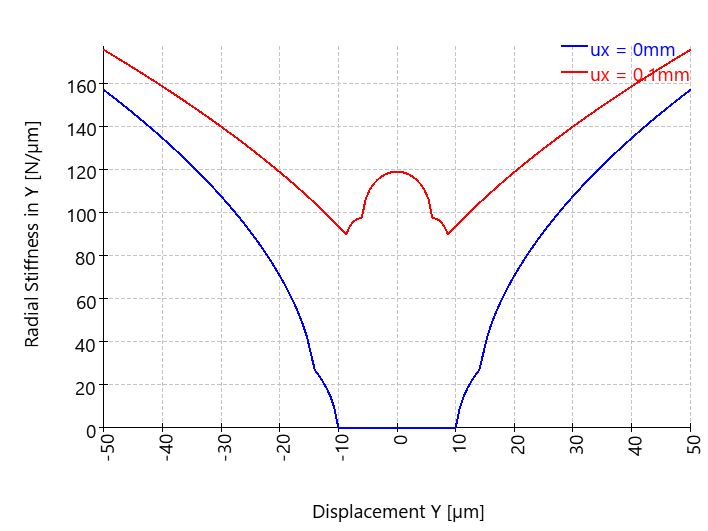
Radial stiffness over radial displacement for two axial displacements
Since the deep groove ball bearing has clearance, the radial force and also the radial stiffness are partially zero. It can be seen that the simple approach of force equals stiffness times displacement does not work for non-linear rolling bearings. The end point of the blue curve is far less than 155*50 = 7750 N, the end point of the red curve is also less than 175*50 = 8750 N. The reason for this is the non-linearity of the bearing stiffness.
The force-displacement curve of the bearing can be described with the tangent stiffness matrix K as follows:
F(u) = F(u0) + K*(u-u0) = F0 + K*u – K*u0 = K*u + (F0 – K*u0)
In order to obtain the correct static deformation in an FEA calculation, the force vector (F0 – K*u0) must be taken into account in addition to the tangent stiffness matrix in order to account for the non-linearity. In the case of linear stiffness, this force vector is zero.
If only natural frequencies are to be calculated and no static solution is required, then the force vector can be omitted. However, the term is required for a correct static solution.


