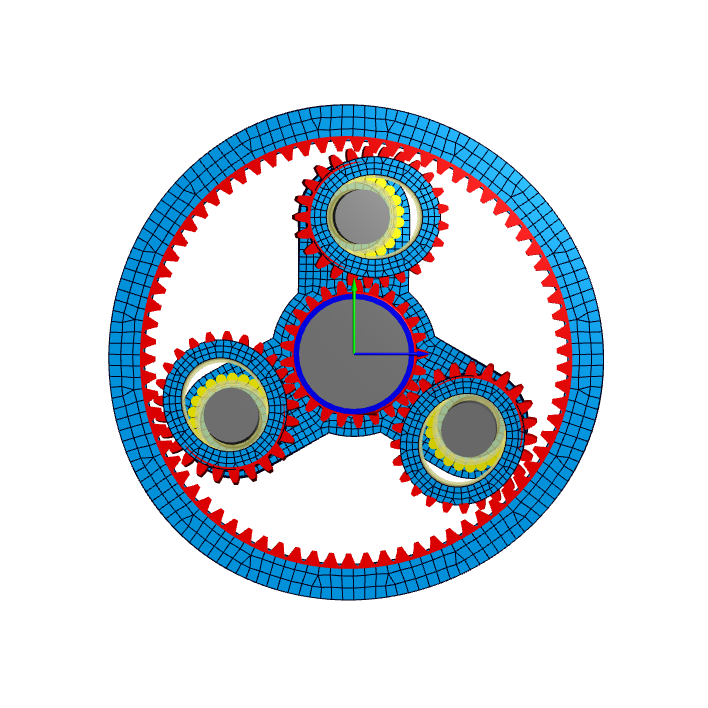
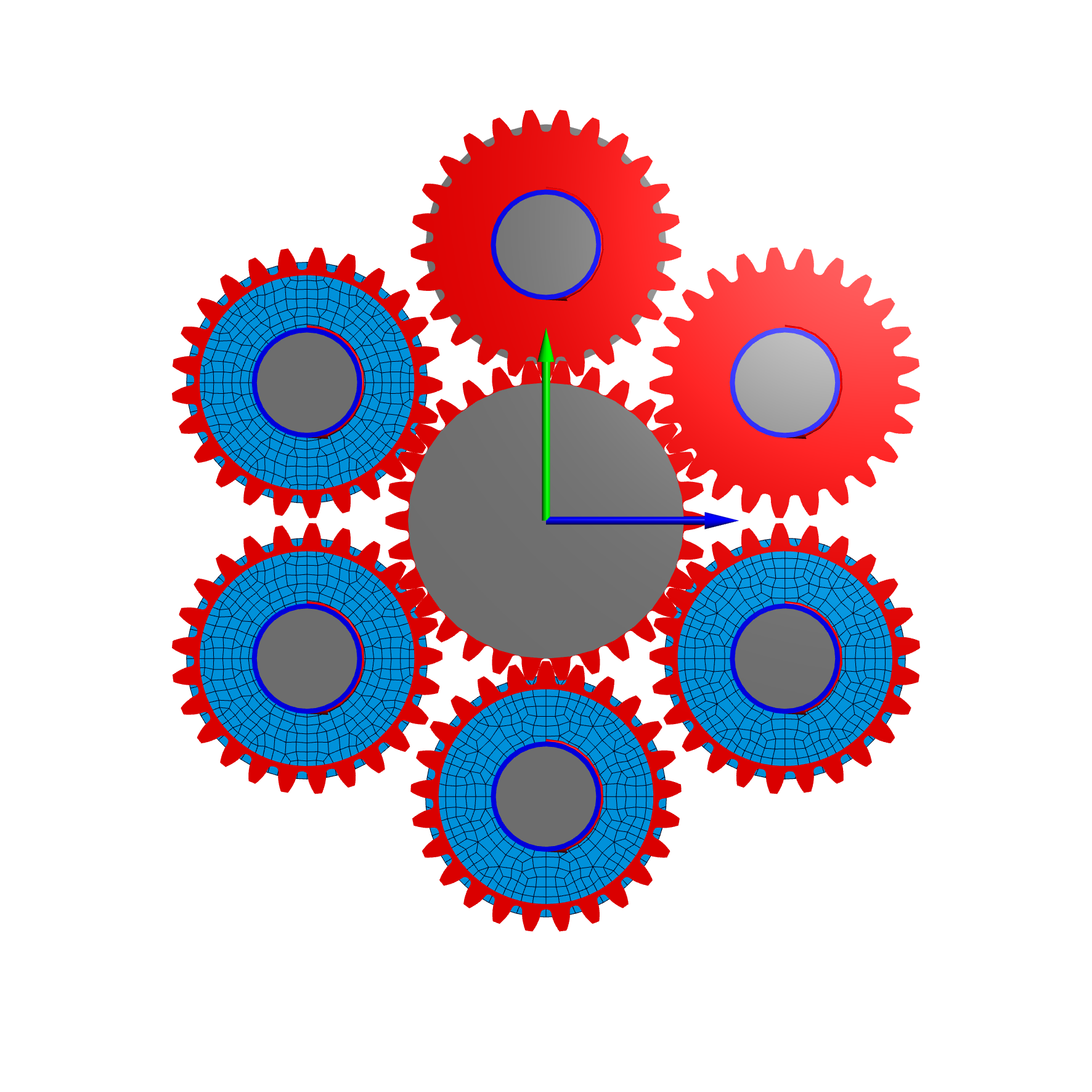
Since version 08/2016 the MESYS shaft system calculation software allows the combination of elastic shafts calculated a 1D-beam-elements with 3D-elastic parts modeled as 3D solid elements. The 3D-elastic parts can be imported CAD geometry or defined parametrically.
The 3D-elastic parts were condensed to single nodes at the interfaces to the shaft model. The next version of the software will additionally allow then coupling of surface deformations for gears and bearings. The deformation of a housing will lead to deformed bearing rings and gear forces will lead to deformations of the gear body. A first example with elastic gears and bearing rings is a planetary stage shown in figure 1.
Gear forces will lead to deformations of the gear body which can affect the load distribution on the flank if the gear tooth is not deformed uniformly. The influence of deformations on the line load distribution of cylindrical in an example of a simple shaft is shown in the following.
The example is a shaft with two rigid supports with a centered gear and with a gear with a small offset from the center.
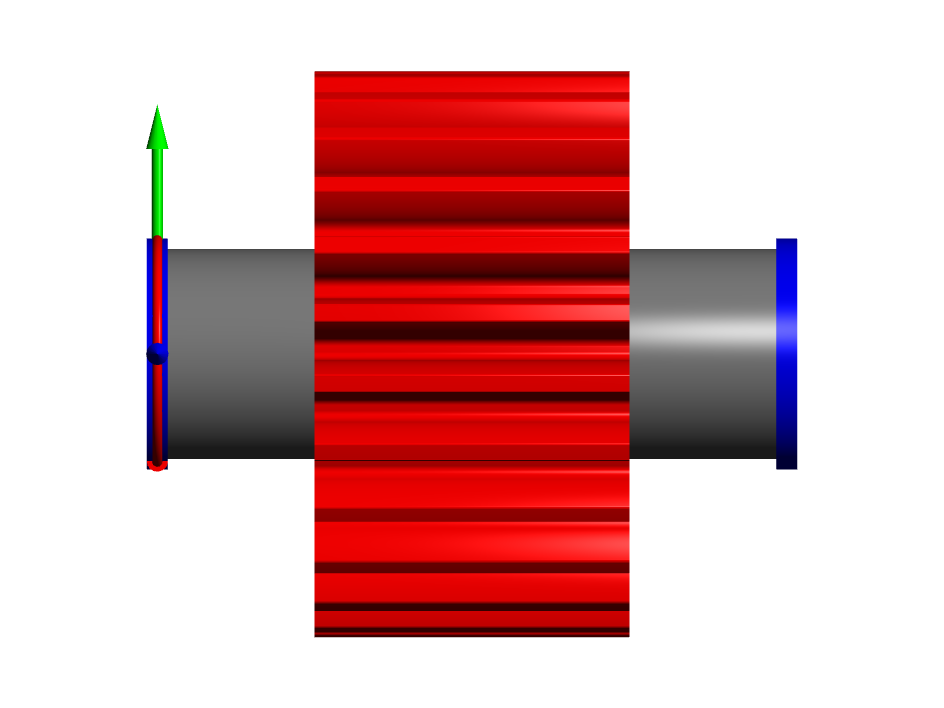

ISO 6336-1 section 7.4.3.2 proposes to use the mean diameter of tip and root diameter for calculation of bending deformations and the root diameter plus 0.4 times module for torsion. Here a rounded value of 48mm (for z=25, mn=2) between these two is used for all calculations. Note that section 7.4.3.3 defines that the shaft is stiffened by a mid diameter between hub diameter and a bore diameter for gears and connections with an interference fit. This mean diameter can be used for the calculation of shaft deformations but not for the calculation of gear deformations as can also be seen in the results below.
| Case | Image | Comment |
|---|---|---|
| 1 | 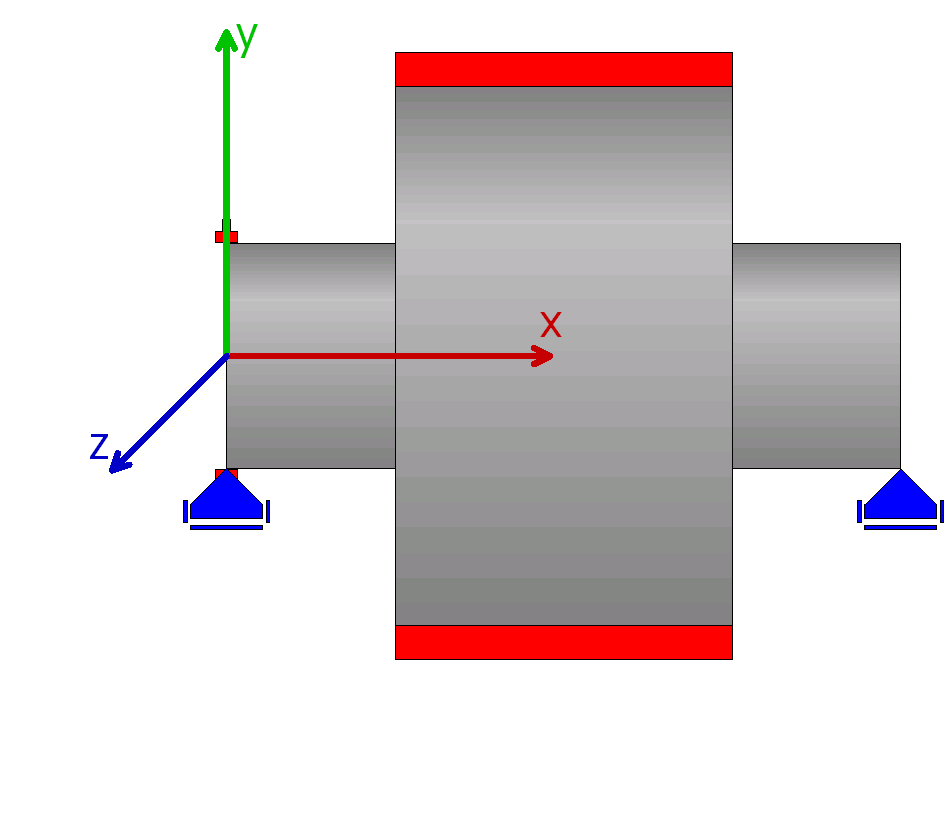 |
The shaft diameter in the range of the gear is increased to a value between root and pitch diameter of the gear. |
| 2 | 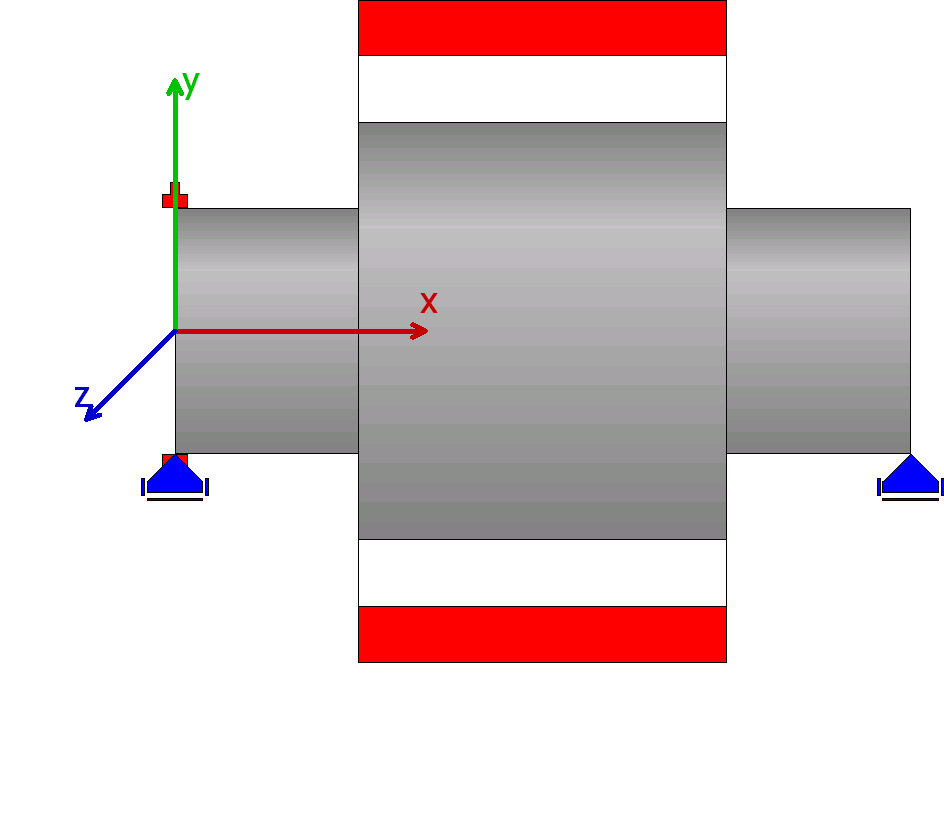 |
The shaft diameter is increases to the mean value of (20+48)/2=34mm. |
| 3 | 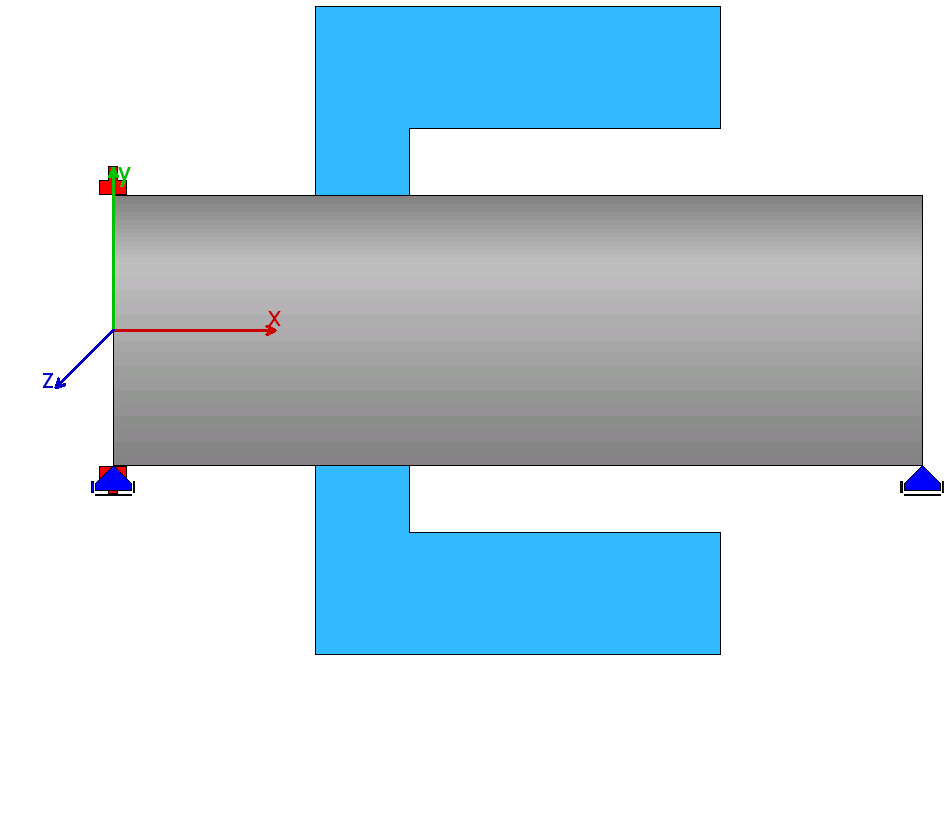 |
An unsymmetric gear body is used which is connected to the shaft in the left. |
| 4 |  |
A full cylinder is used for the gear body. |
| 5 | 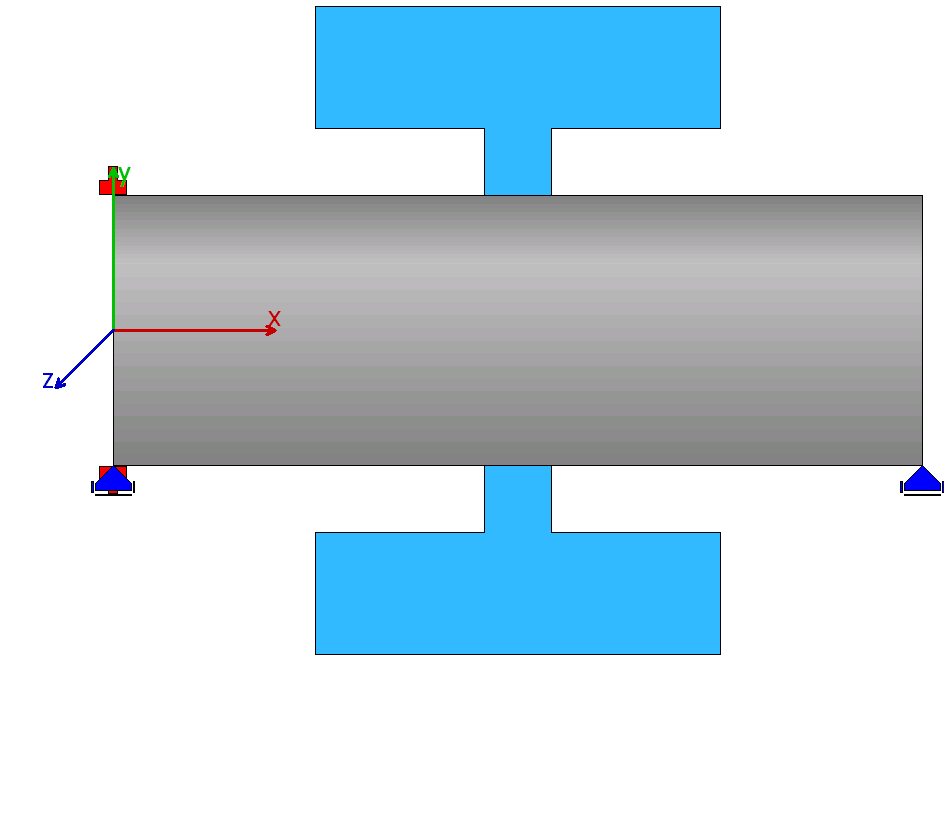 |
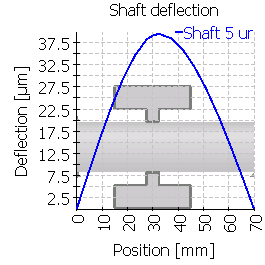
The gear body has a centered rim. |
| 6 | 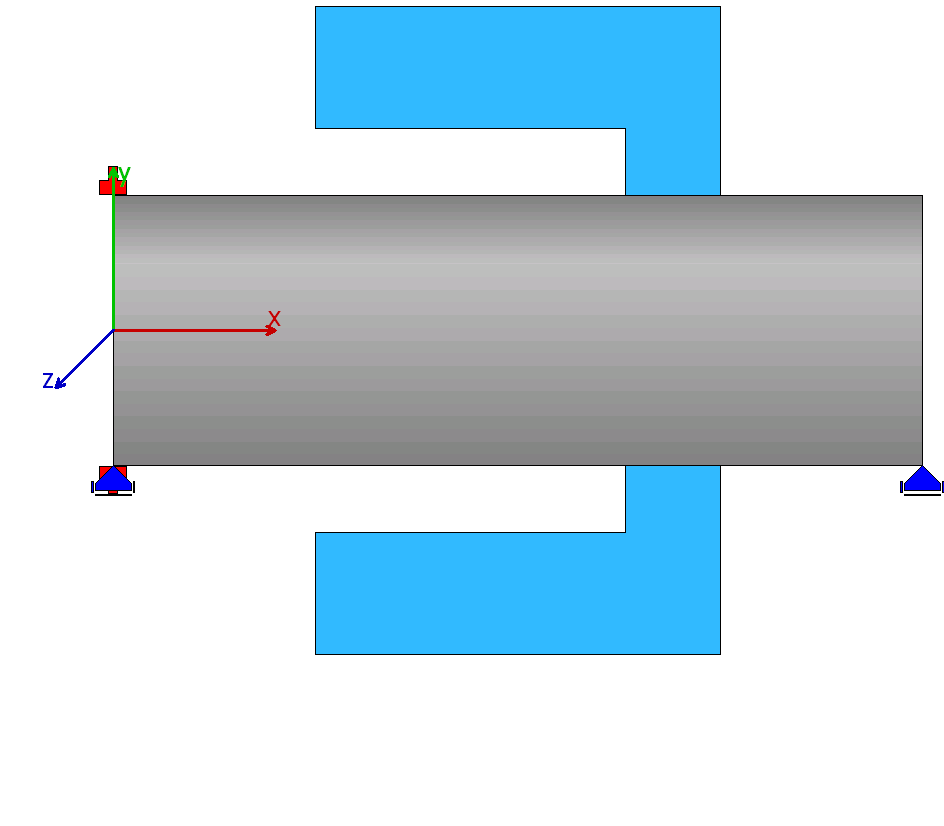 |
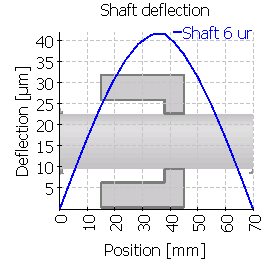
The case 3 is mirrored and a rim on the right is used. |
For the calculation of the gear deformations the gear is in mesh with a second stiff gear which is rigidly supported over the whole width. All six example gears are in contact with this center gear and are loaded with the same torque introduced on the left side of the shaft.
The results are shown for the centric gear and for the eccentric gear:
| Centric gear | 1 | 2 | 3 | 4 | 5 | 6 |
| Maximum shaft deflection [µm] | 6.5 | 8.3 | 26.1 | 9.8 | 26.8 | 26.1 |
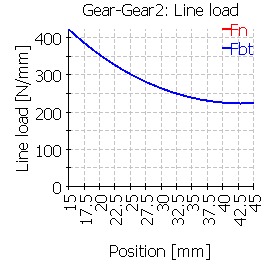
| Line load wmax [N/mm] | 311 | 382 | 566 | 296 | 288 | 566 |
| Ratio wmax/wavg | 1.10 | 1.34 | 2.00 | 1.04 | 1.01 | 1.99 |
| Gap width [µm] | 1.6 | 6.0 | 27.6 | 0.8 | 0.0 | 27.6 |
| Eccentric gear | 1 | 2 | 3 | 4 | 5 | 6 |
| Maximum shaft deflection [µm] | 12.8 | 14.4 | 35.6 | 17.6 | 39.4 | 41.6 |
| Line load wmax [N/mm] | 350 | 423 | 630 | 339 | 333 | 535 |
| Ratio wmax/wavg | 1.23 | 1.49 | 2.22 | 1.19 | 1.17 | 1.89 |
| Gap width [µm] | 5.4 | 9.9 | 34.4 | 5.1 | 5.6 | 24.6 |
The maximum shaft bending is for the inner shaft not considering the gear body. The load ratio wmax/wavg is similar to the face load coefficient, but only load dependent effects are considered and no manufacturing errors. Additional manufacturing tolerances of deflections of the supports would lead to larger face load coefficients. The gap widths is derived from the deformations of the flank line, by virtually rotating the gears back until they have only contact at one point. It should the amount of deformation on the flank line.
Case 1 and 4 both use a fully cylinder as a gear body. The shaft bending of case 4 is larger than of case 1, still the deformations of the flank line are smaller as the gap widths or line load shows. This is because the shaft can deform inside of the gear body. Generally a beam model is too stiff on diameter changes. Many programs for rotor dynamics therefore use a cone for the stiffness diameter on diameter changes. The 3D solid model does consider the stress distribution at these diameter changes automatically without the need to guess average diameters or cone angles.
Case 2 using a mean diameter for the gear body is not useful for the gear deformation like the comparison with case 5 can show. In case of an interference fit the shaft is not stiffened by the gear like in case 5. Still case 5 only shows very little deformation on the flank line. This model with a reduced diameter is only useful for the calculation of the shaft bending line as the shaft bending in case 2 gets larger than in case 1 and closer to case 4.
FThe following table shows the shaft deflection for the six cases with centric and eccentric gear. Note that the scale of the diagrams is different.
| Shaft bending | Centrical gear | Eccentrical gear |
|---|---|---|
| 1 | 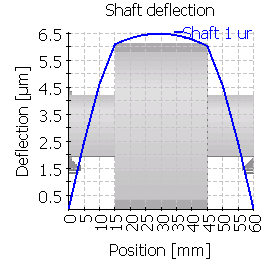 |
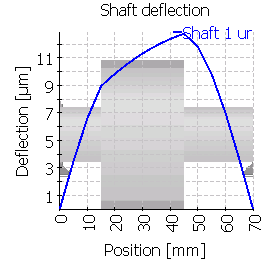 |
| 2 | 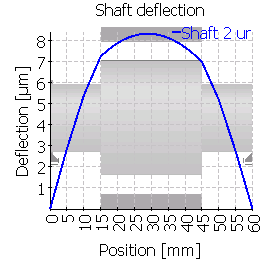 |
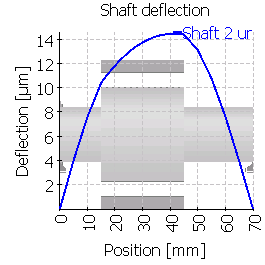 |
| 3 | 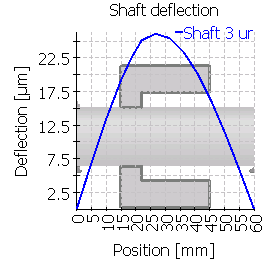 |
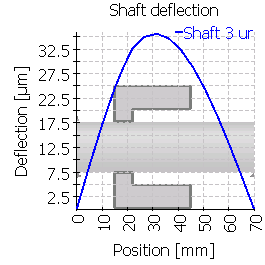 |
| 4 | 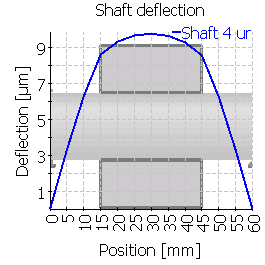 |
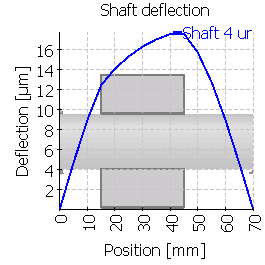 |
| 5 | 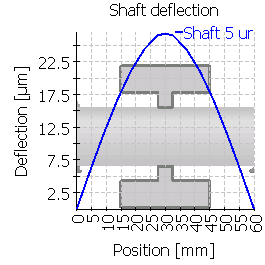 |
 |
| 6 | 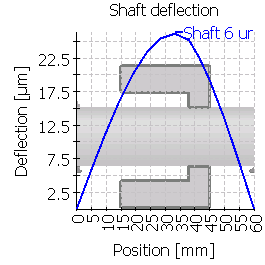 |
 |
The following table shows the line load distribution for the six cases with centric and eccentric gear:
| Line load | Centrical gear | Eccentrical gear |
|---|---|---|
| 1 | 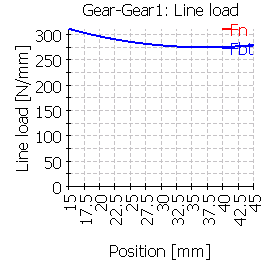 |
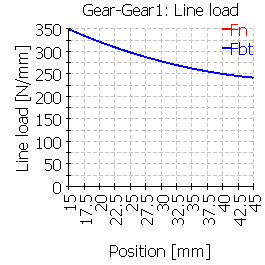 |
| 2 |  |
 |
| 3 | 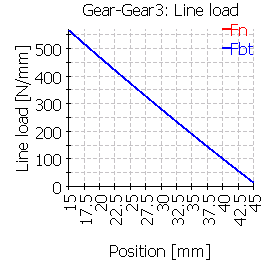 |
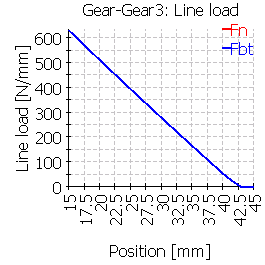 |
| 4 | 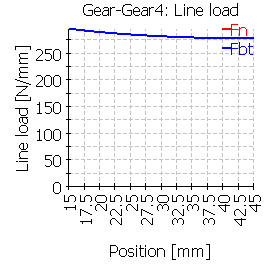 |
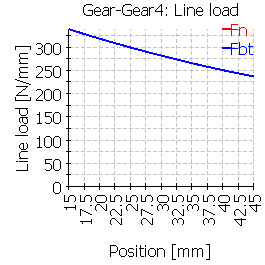 |
| 5 | 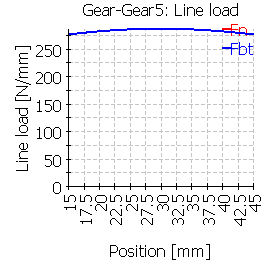 |
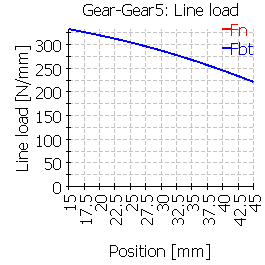 |
| 6 | 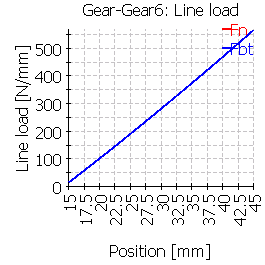 |
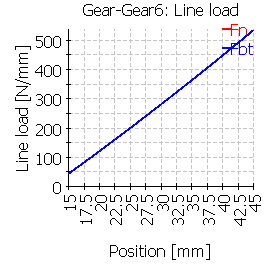 |
In comparison of case 4 and 5 the small influence of the torsion can be seen. While in case 4 with the solid cylinder a small effect of the torque from the left can be seen, case 5 with the rim shows an effect like a small crowning as the outside will be deformed due to torsion and bending.
Cases 3 and 6 show a large misalignment. The main reason on the misalignment is not the deformation of the bear body, but the connection to the shaft at a position of a large tilting angle. The tilting angle of the shaft and the deformation of the gear body are added to the total gear flank deformations in these case, while the other cases see much smaller shaft deflection angles.
Using a more detailed model of a gear body improves the results for the shaft deflection and to the flank line deformations of the gears. In case the simple beam model should be used, the outer diameter of the gear body should be used for calculations for flank line deformations. For a calculation of the shaft deflection a smaller diameter for the gear body can be used and would be a better model for the shaft stiffness.
After a one time static reduction of the gear body which takes about a minute in these cases, the calculation time for the reduced calculation model is still seconds. The only disadvantages is an increased file size for the calculation files.
These examples were shown without any flank line corrections as the influence of deformations on the line load should be shown. Of course the same calculation could also be done including flank line corrections.