If angular contact ball bearings are used the axial clearance of the system has to be determined. This article shows how the parameter variation in the MESYS Shaft Calculation can be used to determine the required axial clearence.
The example shaft with diameter 10mm and speed of 20000 rpm is shown in following image:
Shaft geometry used in the example
As criteria to determine the optimum clearance or pretension the following parameters can be used:
- Bearing life
- Maximum deflection of the shaft
- Natural frequencies of the shaft
- Maximum contact stress within each bearing
- Minimum contact stress within each bearing
- Spin-to-roll-ratio for each bearing
- Ball advance for each bearing
- Friction moment of each bearing
These criteria can be evaluated for a range of temperatures, shaft speeds or tolerances.
Using the parameter variation selected parameters can be varied automatically. The results are shown in tables and in diagrams. In this example the bearing clearance and the temperature are varied. 30 steps for clearance and 1 step for temperature leads to 31*2=62 calculations:
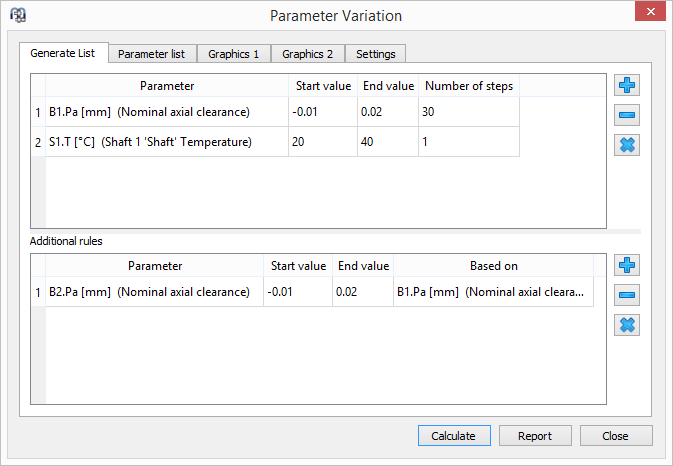
Inputs for the parameter variation
Results can be selected from hundreds of calculation results. A first graphic shows ball bearing life and the first natural freqency for bending of the shaft:
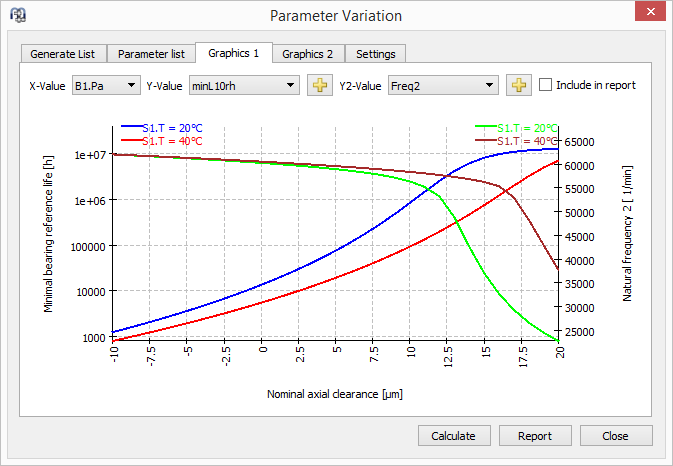
Bearing life and bending natural frequency dependent on bearing clearance
For the natural frequency we get the worst-case for lower temperature but for bearing life the worst-case is at higher temperature. The bearing life decreases with increased temperature because the effect of the radial elongation of the bearing inner ring on clearance is larger than axial elongation of the shaft. Because of the steep decline of the natural frequency we can demand an axial clearance Pa < 12μm. For a bearing life > 20000h the clearance should be larger than 5μm.
A second diagram shows friction moment and spin-to-roll ratio:
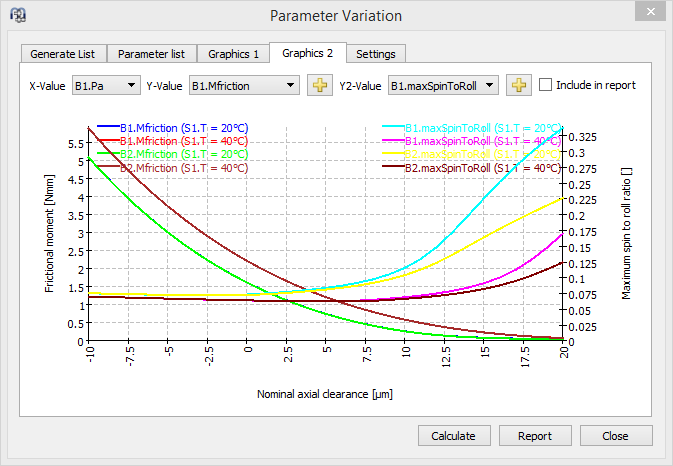
Friction moment and spin-to-roll-ratio dependent on bearing clearance
For the spin-to-roll-ratio often a limit of 0.25 is used. This would lead to an axial clearance Pa < 15μm. A smaller value for spin-to-roll ratio would be even better. The friction moment increases with the pretension (or decreases with the clearance).
As result of both diagrams the axial clearance should be selected as large as possible but smaller than 12μm. The calculation was done with medium tolerances for interference fits and one shaft speed. Now the shaft speed you be varied too and the calculation could be done with maximum/minimum values for interference fits between shaft and bearings. The example used a fixed displacement for pretension. Instead a spring could be used for generating pretension, then the spring stiffness would be another parameter to define.
Because of the high speed the result in this example is a positive bearing clearance. If a low shaft speed would be considered the optimum clearance would be negative, so there would be a pretension.
In addition to bearing life and natural frequencies the shaft calculation software could also calculate shaft strength according DIN 743.


