Profiles can be defined for inner race, outer race and roller.
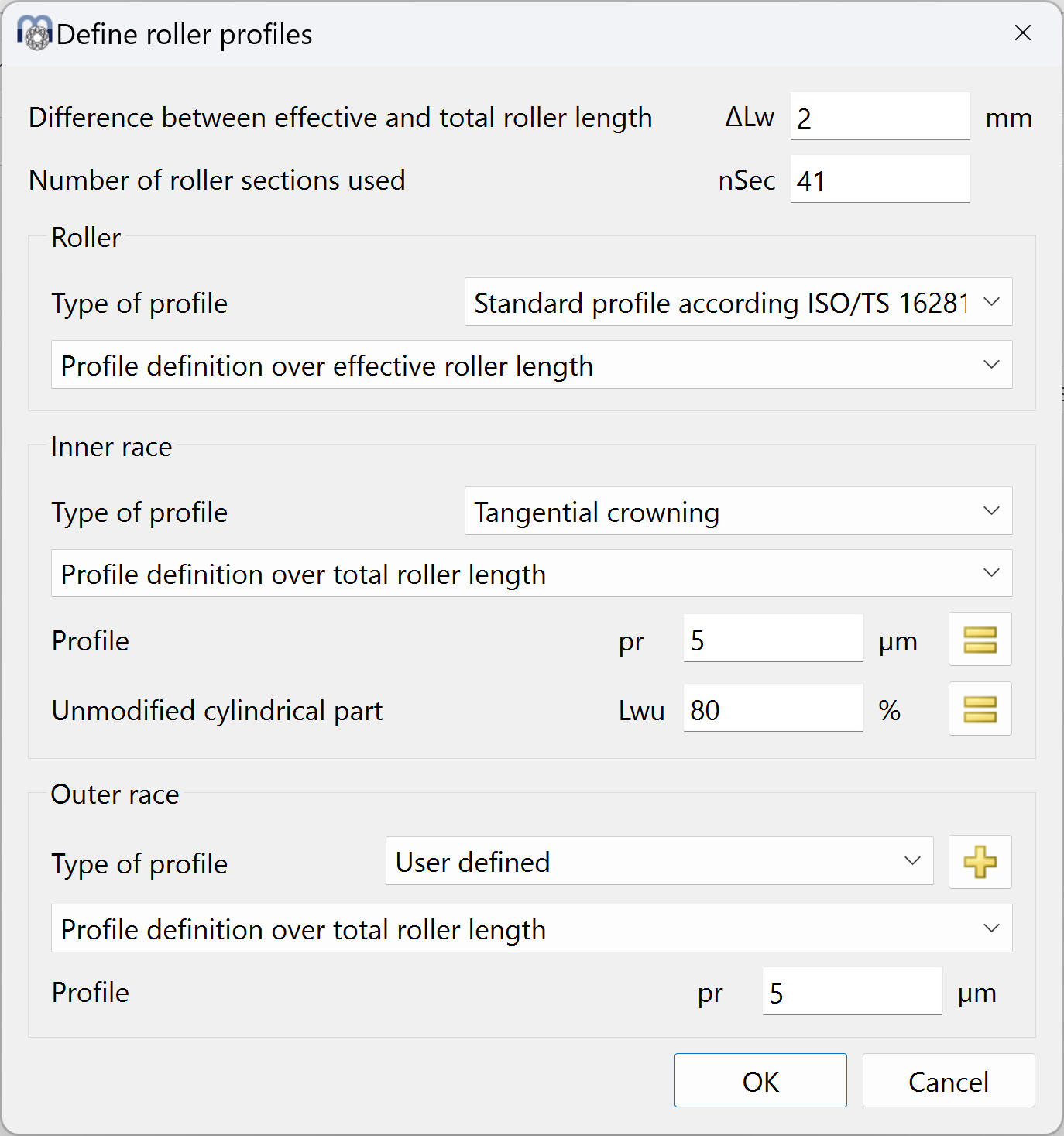
As general inputs, the difference between effective and total roller length can be defined. As it increases the stiffness of the roller, it has an influence on the calculation.
The number of sections for the calculation has to be larger 30 and has to be an odd number. The calculation accuracy and the calculation time increase with a larger number of sections.
Several options are available for the definition of profiles:
1.Standard profile according ISO 16281:
This is using the defaults of the standard, which is logarithmic profile of the roller and no profile on the races.
2.Logarithmic profile:
The amount of relief can be defined and a cylindrical part that should not be modified. The following formula is used:
For the roller, a sizing button provides the default relief according ISO 16281. The default relief of 0.00035*Dw for short cylindrical roller bearings corresponds to a contact stress of 3000MPa.
3.Modified logarithmic profile:
The amount of relief is calculated according following formula derived from (Fujiwara, et al., 2010):
using
The maximum relief is not infinity at the edge of the roller like in the logarithmic profile according ISO 16281 but limited to the maximum value of pr.
Using p = 3000MPa and pr=Infinity, the results are the same as for the logarithmic profile according ISO 16281 above.
The material data for this profile is always taken from the contact roller/inner race.
4.Tangential crowning:
A circular arc tangential to the cylinder is used to generate the profile. The amount of relief and a percentage of unmodified cylinder length can be defined.
5.Crowning:
A circular arc with center positioned axially on the center of the roller is used to generate the profile. The amount of relief and a percentage of unmodified cylinder length and a transition radius can be defined.
6.Two tangential radii:
A first cylindrical part with width "Lwu" is extended by two tangential radii. The width of the first radius is defined as percentage "Lwr1". A requirement is "Lwr1" > "Lwu". "Lwu" can be set to zero to have two radii only.
7.Exponent
An exponent "e" and an unmodified length "Lwu" for the profile can be specified. The exponent has to be . The following formula is used for the profile:
8.Read file:
The profile can be read from a file. The data has to be specified with two values on each line, an axial position and the profile relief. The axial position is scaled with the roller length and the relief is scaled with the input for the profile relief. So a range from -1 to +1 can be used for the axial position and 0 to 1 for the relief.
A very simple file is shown here. It was selected for the inner race profile on the right:
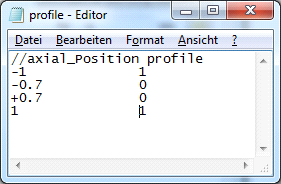
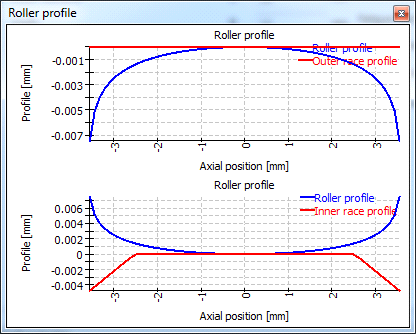
The unsymmetrical profile is used from left to right for most bearings. For taper roller bearings and axial spherical roller bearings, the profiles is used from left to right if direction of contact angle is left. For contact angle to the right, the profile is mirrored. So mounting conditions do not influence the profile.
9.Read file without scaling:
Like option "Read file" the data is read from a file. Using this option no scaling will be done. The axial extension has to be defined from -Lwe/2 to +Lwe/2 or from 0 to Lwe. The profile is defined in "mm" and won't be scaled too.
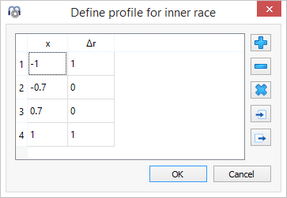
10.User Input:
Instead of defining a file name, the points for the profile can be defined in a table. Again as above, use a range of -1 to +1 for the axial position and a value between 0 and 1 for the profile relief.
The table in the diagram on the right shows the same data as the file above.
11.User defined equation:
A user defined equation can be defined in ECMAScript language. The variable 'x' has the range and variables 'Dw', 'Lwe', 'Lw' are defined and in 'mm'. The result of the equation is considered in 'mm' and a positive value increases the gap.
Examples are "return 0.01*x**4;" or "return -0.00035*Dw*Math.log(1-x*x);" or using conditions like
if(x < -0.5) {
return 0.01*(-0.5-x);
}
if(x > 0.5) {
return 0.01*(x-0.5);
}
return 0;